动作价值函数(基于价值)

• Cumulative Discounted Future Reward

$$ U_t = \sum_{n=0}^{…} \gamma^{n} R_{t+n} $$

Return UT 依赖于之后的状态S动作A

• 动作价值函数$Q_\pi$

$\pi$是策略, 于是动作价值函数可以表达为

$$Q_\pi(s_t, a_t)=E[U_t|S_t=s_t, A_t=a_t]$$

取最大得到最优动作价值函数(optimal action-value function):

$$Q^*(s_t, a_t)=\max_{\pi}Q_\pi(s_t, a_t)$$

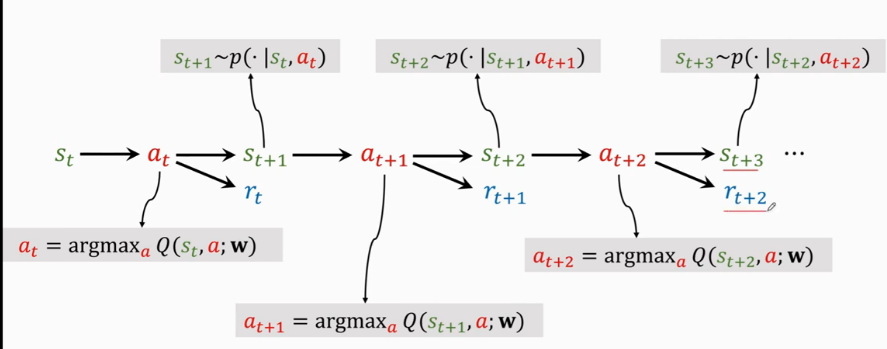
• 最优动作$a^=\argmax_aQ^(s_t,a_t)$

基于动作价值函数训练Q-function令$Q(s,a;w)\approx Q^*(s,a)$

• 训练QDN: TD(Temporal Difference Learning)

TD算法核心$T_{estimateOverall} \approx T_{realAtoMid} + T_{estimateMidtoB}$

$$\to Q(s_t,a_t;w) \approx r_t + \gamma Q(s_{t+1},a_{t+1};w)$$

其中$r_t$为当前时刻价值的ground truth

该推论可通过折扣回报的展开得到, 公式来源于Q的自治条件

TD的目标是让$Q(s_t,a_t;w)$无限接近于公式的后半部分

$$ y_r = r_t + \gamma Q(s_{t+1},a_{t+1};w)\
L_{t} = \frac{1}{2}[Q(s_t,a_t;w) - y_t]^2\
w_{t+1} = w_{t} - \alpha \cdot \frac{\partial L_t}{\partial w}|_{w=w_t} $$

通过梯度下降就可以学习w

状态价值函数(基于策略)

• 策略函数 $\pi(a|s)$输出为当前状态选择a的概率

参数化策略函数$\pi(a|s;\theta)$ $\theta$是可训练参数

• 状态价值函数

$$V_\pi(s_t)=E_A[Q_\pi(s_t,A)]=\sum_a \pi(a|s_t) \cdot Q_\pi(s_t,a), \space (A \sim \pi(\cdot|s_t))$$

$$V_\pi(s_t;\theta)=\sum_a \pi(a|s_t;\theta) \cdot Q_\pi(s_t,a)$$

目标是最大化$J(\theta)=E_S[V_pi(S;\theta)]$, 这里采用策略梯度下降(不严谨推导–ShusenWang)

• 采样s
• $\theta \gets \theta + \beta \frac{\partial V(s;\theta)}{\partial \theta}$

$$\frac{\partial V(s;\theta)}{\partial \theta} = \sum_a\frac{\partial \pi(a|s;\theta)}{\partial \theta}\cdot Q_\pi(s,a)=\sum_a\pi(a|s;\theta)\frac{\partial log\pi(a|s;\theta)}{\partial \theta}\cdot Q_\pi(s,a)=E_A[\frac{\partial log\pi(A|s;\theta)}{\partial \theta}\cdot Q_\pi(s,A)], Q_\pi \space independent \space with \space \theta$$

对于连续变量采用蒙特卡罗近似近似上述期望

Q的近似:

• Reinforce

• Actor-Critic(AC同时近似了V和Q, 实际上是两个神经网络)

小结

强化学习的实际上是通过近似价值函数来优化当前动作以取得期望收益的最大化, 其中又分为基于价值和基于策略的方法. 价值方法使用动作价值函数Q, 训练Q的权值矩阵w, 令价值函数近似ground truth, 选取价值最大的动作; 而策略方法使用状态价值函数V, 训练$\pi$的权值矩阵$\theta$, 通过令$V_\pi(s;\theta)$近似ground truth(即最大化), 优化策略本身.